the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Prediction of internal egg quality characteristics and variable selection using regularization methods: ridge, LASSO and elastic net
Mehmet Nur Çiftsüren
Suna Akkol
This study was conducted to determine the inner quality characteristics of eggs using external egg quality characteristics. The variables were selected in order to obtain the simplest model using ridge, LASSO and elastic net regularization methods. For this purpose, measurements of the internal and external characteristics of 117 Japanese quail eggs were made. Internal quality characteristics were egg yolk weight and albumen weight; external quality characteristics were egg width, egg length, egg weight, shape index and shell weight. An ordinary least square method was applied to the data. Ridge, LASSO and elastic net regularization methods were performed to remove the multicollinearity of the data. The regression estimating equations of the internal egg quality were significant for all methods (P<0.01). The goodness of fit of the regression estimating equations for egg yolk weight was 58.34, 59.17 and 59.11 % for the ridge, LASSO and elastic net methods, respectively. For egg albumen weight the goodness of fit of the regression estimating equations was 75.60 %, 75.94 % and 75.81 % for the respective ridge, LASSO and elastic net methods. It was revealed that LASSO, including two predictors for both egg yolk weight and egg albumen weight, was the best model with regard to high predictive accuracy.
- Article
(177 KB) - Full-text XML
- BibTeX
- EndNote
The egg production industry has significant economic value as well as being a remarkable source of employment. Consequently, it has an important place in the development of countries' economies and in meeting the nutritional needs of people worldwide. Determination of egg quality is a requirement for both edible eggs and for the production of hatching eggs. Egg quality is examined in two parts in this study, with focus on both internal and external quality characteristics. Previous research has pointed out that egg weight, shell weight, shell thickness, egg yolk weight, albumen weight, the albumen index, the egg yolk index and the Haugh units are all significant factors affecting egg quality (Uluocak et al., 1995; Khurshid, 2003; Alkan et al., 2010). These egg characteristics are highly correlated and are used for the determination of the relationship between internal and external quality of eggs (Khurshid et al., 2003; Kul and Şeker, 2004; Abanikannda et al., 2007; Üçkardeş et al., 2012).
In multiple linear regression analysis based on the ordinary least squares (OLS) method, this high correlation between independent or predictor variables can lead to the issue of multicollinearity (MC) (Montgomery et al., 2001; Şahinler, 2000). It has been reported that this MC problem causes a reduction in the reliability of estimates, as it expands the standard errors of the regression coefficients (Montgomery et al., 2001, Albayrak, 2005; Yakubu, 2010). As a result of this, although the OLS estimates are still unbiased in the model with the MC issue, it is not clear how the various egg weight measurements are affected by the egg components.
Various methods to overcome the MC problem are discussed in the literature. One of the methods used in such cases is ridge regression (Hoerl and Kennard, 1970), which is a regularization method that has been used by a number of researchers (Topal et al., 2010; Üçkardeş et al., 2012; Shafey et al., 2014; Orhan et al., 2016). Another regularization method is the least absolute shrinkage and selection operator, “LASSO” (Tibshirani, 1996). LASSO is a successful continuous procedure for estimating and selecting variables (Tibshirani, 1996; Efron et al., 2004; Hastie et al., 2007). This method has been successfully used by Kominakis et al. (2009), Ogutu et al. (2012), Acharjee et al. (2013) and Amin et al. (2014). However, LASSO has two important limitations which emerge in cases where the number of variables is too large for the number of observations (k>n), and when the pairwise correlations of a group of variables are high (Efron et al., 2004). The elastic net (EN) method, proposed by Zou and Hastie (2005), eliminates the shortcomings of the LASSO method. While this method works like LASSO when choosing a variable, it functions like ridge by bringing the coefficients of correlated predictors closer to each other (Hastie et al., 2008). There is currently no known study demonstrating the use of the LASSO and EN methods in order to determine the internal quality characteristics of eggs.
Table 1Descriptive statistics of egg quality characteristics.
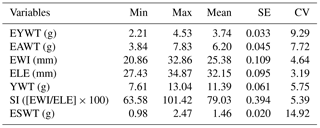
Min: minimum value; Max: maximum value; SE: standard error; CV: coefficient
of variation; EYWT: egg yolk weight; EAWT: egg albumen weight; EWI: egg
width;
ELE: egg length, EWT: egg weight; SI: shape index; and ESWT: egg shell
weight.
Table 2Correlation coefficients between internal and external quail egg quality characteristics and between variance inflation factors and tolerance values.
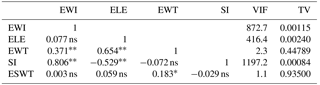
* p<0.05; P<0.01; ns: not significant; EWI: egg width; ELE: egg length; EWT: egg weight; SI: shape index; ESWT: egg shell weight; VIF: variance inflation factor; and TV: tolerance value.
Table 3Eigenvalues and conditional index values of external egg quality characteristics predicting EYWT and EAWT.

E: eigenvalue and CI: conditional index.
Therefore, the aims of this study were to determine egg yolk weight and albumen weight from external egg quality characteristics using the ridge, LASSO and EN regression models and to select the variables in order to reduce model complexity.
2.1 Materials
The materials utilized in this study were 117 eggs taken from Japanese quails; the eggs were obtained from the Van Yuzuncu Yil University Research and Application Farm. Egg weight (EWT), egg yolk weight (EYWT), egg albumen weight (EAWT) and shell weight (ESWT) (in grams) and egg width (EWI) and egg length (ELE) (in mm) were the variables measured, with the eggs collected daily. Shape index (SI) is a value that depends on EWI and ELE; SI was calculated using the following equation: SI = [EWI/ELE]×100. EWI, ELE, EWT, SI and ESWT were used as predictor variables in the models that were created separately for EYWT and EAWT.
2.2 Methods
2.3 Ordinary least squares
For the multiple linear regression model with as many independent variables as k for n individuals, the following equation was used for OLS prediction:
where is the OLS estimation of unknown parameters in the regression equation, yi is the dependent variable (, β0 intercept and βj ( show the unknown parameters of the regression equation and xij indicates the explanatory or predictor variables.
2.4 Ridge
Ridge, a biased prediction method, is based on the principle of minimizing the sum of the residual squares (RSS) in order to obtain the β coefficients. The following equation is used to obtain the ridge coefficients:
where λ≥0 is the complexity constant controlling the amount of shrinkage (Marquardt, 1970), and is the ridge penalty function (Hastie et al., 2008).
2.5 LASSO
In this method, it is possible to obtain β coefficients by solving the following optimization problem:
where is the LASSO penalty function. ℓ1 penalty is the least squares fit and shrinks some components of to zero. The solution of the LASSO method requires quadratic programming (Hastie et al., 2007).
2.6 Elastic net (EN)
Elastic net is an extension of the LASSO method that is robust to extreme correlations among the predictors (Friedman et al., 2010). The method uses a mixture of the ridge (ℓ2) and LASSO (ℓ1) penalties and can be formulated as follows:
Goodness off fit. The adjusted coefficients of determination ( were used as cohesion criteria to compare the ridge, LASSO and EN methods:
In Eq.5, R2 represents the determination coefficient, n represents the sample size and p represents the total number of explanatory variables in the model not including the constant.
The statistical analyses were performed using the GLMSELECT procedure in SAS/STAT (SAS, 2014).
The descriptive statistics of the egg quality characteristics are shown in Table 1. EYWT, EAWT, EWI, ELE, EWT, SI and ESWT averaged 3.74 g, 6.20 g, 25.38 mm, 32.15 mm, 11.39 g, 79.03 % and 1.46 g, respectively.
Table 4The estimation of coefficients obtained using the OLS, ridge, LASSO and EN methods in the multiple linear regression analyses (standard errors in parentheses) for EYWT and EAWT.
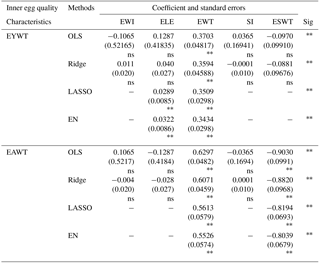
P<0.01 and ns: not significant.
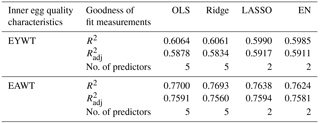
Table 5Goodness of fit measurements of OLS, ridge, LASSO and EN methods in multiple linear regression analyses.
The Pearson correlation coefficient between internal and external quality characteristics of quail eggs and MC diagnostics, variance inflation factors (VIFs) and tolerance values (TVs) are given in Table 2. Eigenvalues and conditional index (CI) values, the other criteria used to determine MC, are presented in Table 3. The respective correlations between EWI and EWT and EWI and SI were 0.371 and 0.806 (P<0.01), the respective correlations between ELE and EWT and ELE and SI were 0.654 and −0.529 (P<0.01) and the correlation between EWT and ESWT was 0.183 (P<0.05). The VIF values for EWI, ELE and SI were very high, 872.7, 416.4 and 1197.2, respectively, and TV values for these variables were close to zero, 0.00115, 0.00240 and 0.00084, respectively. In Table 3 it can be seen that the eigenvalues are close to zero (ranging from 0.018 to 6.18 × 10−7) and the CI values are very high (ranging from 17.98 to 3109.37).
The prediction equations of the internal quality characteristics obtained using the OLS, ridge, LASSO and EN methods in the multiple linear regression analyses are given in Table 4. For all of the methods, the prediction equations are found significant (P<0.01). When Table 4 is examined, it can be seen that the standard errors in ridge for EYWT show a significant decrease with the exception of EWT and ESWT. A similar result is also found for EAWT. When the results of LASSO and EN are evaluated, it is seen that the coefficients of EWI, SI and ESWT are reduced to zero for EYWT and the coefficients of EWI, ELE and SI are reduced to zero for EAWT.
The goodness of fit measurements of the prediction equations for the OLS, ridge, LASSO and EN methods and the number of predictors in the prediction are presented in Table 5. There are five predictor variables in OLS and ridge and two in LASSO and EN both for EYWT and EAWT.
Table 5 shows that the values for EYWT are 58.34, 59.17 and 59.11 % for ridge, LASSO and EN, respectively; whilst the EAWT values for the for ridge, LASSO and EN methods are 75.60, 75.94 and 74.81 %, respectively.
When the data used in the study were evaluated in terms of basic statistics, EYWT, EAWT, EWI, ELE, EWT and SI were found to be similar to the findings of Kul and Şeker (2004) (Table 1). However, the mean value of ESWT was 1.46 ± 0.02, which was higher than that reported by Kul and Şeker (2004) (0.84 ± 0.01).
The results of the correlation analyses showed that high and significant correlations were obtained between the predictor variables: the correlation between EWI and SI was 0.806 (P<0.001), the correlation between ELE and EWT was 0.654 (P<0.001) and the negative correlation between ELE and SI was 0.529 (P<0.001). Table 1 shows that it was necessary to investigate the MC problem. Similar findings have also been reported in a variety of studies on the internal and external quality characteristics of eggs, such as those by Özçelik (2002), Kul and Şeker (2004), Alkan et al. (2010) and Rathert et al. (2011).
In order to investigate the MC problem, the VIFs and TVs in Table 2, the eigenvalues and CI values in Table 3 were calculated using the OLS method. This was undertaken because it is known that the correlation between the predictor variables is not sufficient to define the MC issue (Albayrak, 2005; Shafey et al., 2014). The OLS results showed that VIF values were greater than 10 in 3 variables: 872.7, 416.4 and 1197.2 for EWI, ELE and SI, respectively. The TVs values were found to be small, depending on the VIFs due to the relationship between the two. The high VIF values were caused by the small tolerance value, as reported by Albayrak (2005). The eigenvalues were very close to zero (down to 6.18 × 10−7) and the CI values were greater than 30 (up to 3109.37). All of these results revealed that there was in fact a MC problem in the dataset as reported by Marquardt and Snee (1975), Belsley (1991) and Albayrak (2005).
The aims of this study were to determine the internal quality characteristics of eggs and to choose variables using the external quality characteristics of eggs. As previous studies have proven that OLS estimates are less reliable if the data has an MC problem (Hoerl and Kennard, 1970; Montgomery et al., 2001; Albayrak, 2005; Yakubu, 2010), ridge regression was applied to the data to eliminate the MC issue (Table 4). The results of the regression analyses for both EYWT and EAWT were found to be significant (P<0.001). The coefficients and standard errors of EWI, ELE, EWT, SI and ESWT in the prediction equations for EYWT and EAWT were smaller than those in the OLS prediction (Table 4); in particular, the sign of the coefficients of EWI and SI changed. All of these results were similar to those found in the literature (e.g., Topal et al. (2010); Üçkardeş (2012) and Öztürk (2014)). Due to the fact that ridge regression is not a sufficient method for selecting variables, LASSO and EN were applied to the data. Only two predictor variables were included in the prediction equations of LASSO and EN (ELE and EWT for EYWT; EWT and ESWT for EAWT) and the regression equations were both found to be significant (P<0.001, Table 4). Both methods provided similar results in terms of coefficients and standard errors. The coefficients and the standard errors of ELE and EWT in both EN and LASSO were smaller than those in ridge for EYWT. Apart from the standard error of EWT in ridge, similar results were obtained for EAWT (Table 4). These results revealed that LASSO and EN performed better than ridge regression in this study, which was consistent with the study by Ogutu et al. (2012).
The goodness of fit statistics used in order to find the best models are only given for OLS and the regularization methods (Table 5). Since the number of parameters in the prediction equations obtained by the regularization methods were different from one another, was used to compare the methods. Therefore, for EYWT, the predictive ability as depicted by was highest using the LASSO method (59.17 %) and lowest using the ridge method (58.34 %). This was similar for EAWT, where was highest in LASSO (75.94 %) and lowest in ridge (75.60 %). Therefore, for both EYWT and EAWT, the LASSO technique succeeded in selecting the variables with the highest predictive ability. Zou and Hastie (2005) found that EN performed better than ridge and LASSO in terms of model choice consistency and predictive accuracy in their study. However, this result is only valid under two conditions: (1) that the data being studied contain more predictor variables than the number of observations (k>n) and (2) that there is a group of variables among which the pairwise correlations are very high. The materials used in this study do not have these conditions. In this research, a simpler prediction equation, which is both highly predictive and easy to interpret, was obtained using the LASSO technique. These results were also found to be consistent with the literature (Efron et al., 2004; Zou and Hastie, 2005; Friedman et al., 2010).
The determination of internal egg quality characteristics is important in terms of edible eggs and the production of hatching eggs. In this study the ridge, LASSO and EN regularization methods were used in order to perform prediction equations and variable selection for both EYWT and EAWT. It was revealed that LASSO, including two predictors in the prediction equation, was the best model with regard to high predictive accuracy. It was concluded that ELE and EWT were included in the prediction equation for EYWT, while EWT and ESWT were included for EAWT.
Regularization methods are superior to OLS in data with a MC problem because, when these methods are used, more accurate and reliable prediction equations are obtained. In this study we introduced the LASSO and EN methods for prediction and variable selection in agricultural research. It is concluded that LASSO and EN techniques may be utilized to develop the best and most stable models for internal egg quality characteristic prediction using external egg quality characteristics because they overcome the MC problem. These techniques also enable the selection of sufficient variables in order to obtain models that are easily interpreted by researchers.
A total of 117 Japanese layer quails (Coturnix coturnix japonica) being raised on the Van Yuzuncu Yil University Research and Application Farm were used in the study. All quails were fed on a basal diet that contained 2679 kcal ME kg−1, 17.8 % CP and 3.5 % calcium. The eggs were collected at 8 weeks of age and measurements were made in the lab.
The authors declare that they have no conflict of interest.
This study based on the first author's master's thesis (Çiftsüren,
2017) and was financially supported by the Van Yuzuncu Yil University Scientific
Research Projects Directorate (project no. FYL-2016-5034).
Edited by: Manfred Mielenz
Reviewed by: Nazire Mikail and one anonymous referee
Abanikannda, O. T. F., Olutogun, O., Leigh, A. O., and Ajayi, L. A.: Statistical modeling of egg weight and egg dimensions in commercial layers, Int. J. Poult. Sci., 6, 59–63, 2007.
Acharjee, A., Finkers, R., Visser, R. G. F., and Maliepaard, C.: Comparison of regularized regression methods for ∼omics data, Metabolomics, 3, 1–9, https://doi.org/10.4172/2153-0769.1000126, 2013.
Albayrak, S. A.: Çoklu bağlantıhalinde en küçük kareler teknikleri ve bir uygulama, Zonguldak Kara Elmas Üniversitesi, Sosyal Bilgiler Dergisi, 1, 105–126, 2005.
Alkan, S., Karabağ, K., Galiç, A., Karslı, T., and Balcıoğlu, M. S.: Effects of selection for body weight and egg production on egg quality traits in Japanese quails (Coturnix coturnix japonica) of different lines and relationships between these traits, Kafkas Üniversitesi Veteriner Fakültesi Dergisi, 16, 239–244, https://doi.org/10.9775/kvfd.2009.633, 2010.
Amin, M., Xiaoguang, W., Song, L., Ullah, H., and Ashraf, M. Y.: Penalized selection of variable contributing to enhanced seed yield in mungbean (Vigna radiata L.), Pakistan Journal of Agriculture Science, 51, 373–381, 2014.
Belsley, D. A.: Conditioning Diagnostics, Collinearity and Weak Data in Regression, John Wiley and Sons, New York, NY, USA, 1991.
Efron, B., Hastie, T., Johnstone, I., and Tibshirani, R.: Least angle regression, The Annals of Statistics, 32, 407–499, 2004.
Friedman, J., Hastie, T., and Tibshirani, R.: Regularization paths for generalized linear models via coordinate descent, J. Stat. Softw., 33, 1–22, 2010.
Hastie, T., Taylor, J., Tibshirani, R., and Walther, G.: Forward stagewise regression and the monotone lasso, Electron. J. Stat., 1, 1–29, https://doi.org/10.1214/07-EJS004, 2007.
Hastie, T. J., Tibshirani, R., and Friedman, J.: The Elements of Statistical Learning: Prediction, Inference and Data Mining, 2nd edn. Springer Verlag California, 2008.
Hoerl, A. E. and Kennard, R. W.: Ridge regression: biased estimation for non-orthogonal problems, Technometrrics, 12, 55–82, https://doi.org/10.1080/00401706.1970.10488634, 1970.
Khurshid, A., Farooq, M., Durrani, F. R., Sarbiland, K., and Chand, N.: Predicting egg weight, shell weight, shell thickness and hatching chick weight of Japanese quails using various egg traits as regressors, International Journal of Poultry Science, 2, 164–167, https://doi.org/10.3923/ijps.2003.164.167, 2003.
Kominakis, A. P., Papavasiliou, D., and Rogdakis, E.: Relationships among udder characteristics, milk yield and, non-yield traits in Frizarta dairy sheep, Small Ruminant Researc., 84, 82–88, https://doi.org/10.1016/j.smallrumres.2009.06.010, 2009.
Kul, S. and Şeker, İ.: Phenotypic correlations between some external and internal egg quality traits in the japanese quail (Coturnix coturnix japonica), International Journal of Poultry Science, 3, 400–405, https://doi.org/10.3923/ijps/2004.400.405, 2004.
Marquardt, D. W. and Snee, R. D.: Ridge Regression in Pratice, The American Statistician, 29, 3–20, https://doi.org/10.2307/2683673, 1975.
Marquardt, D. W.: Generalized invers, ridge regression, biased linear estimation and nonlinear estimation, Techonometrics, 12, 591–612, https://doi.org/10.1080/00401706.1970.10488699, 1970.
Montgomery, D. C., Peck, E. A., and Vining, G. G.: Introduction to Linear Regression Analysis, 3rd Edition, John Wiley & Sons, New York, 2001.
Ogutu J. O., Schulz-Streeck T., and Piepho, H. P.: Genomic selection using regularized linear regression models: ridge regression, lasso, elastic net and their extensions, BMC Proceedings, 6, p. S10, https://doi.org/10.1186/1753-6561-6-S2-S10, 2012.
Orhan, H., Eyduran, E., Tatliyer, A., and Saygici, H.: Prediction of egg weight from egg quality characteristics via ridge regression and regression tree methods, Revista Brasileira de Zootecnia, 45, 380–385, https://doi.org/10.1590/S1806-92902016000700004, 2016.
Özçelik, M.: Japon bıldırcınıyumurtalarında bazıiç ve dış kalite özellikleri arasındaki fenotipik korelasyonlar, Ankara Üniversitesi Veterinerlik Fakültesi, 49, 67–62, 2002.
Öztürk, İ.: Hayvansal üretim verilerinde çoklu bağlantıprobleminin yanlıregresyon yöntemi ile çözümlenmesi, Kahramanmaraş Sütçü İmam Üniversitesi Doğa Bilimleri Dergisi, 17, 1–12, 2014.
Rathert, T. Ç., Üçkardeş, F., Narinç, D., and Aksoy, T.: Comparision of Principal Component Regression with the Least Square Method in Prediction of Internal Egg Quality Characteristics in Japanese Quails, Kafkas Universitesi Veteriner Fakultesi Dergisi, 17, 687–692, https://doi.org/10.9775/kvfd.2010.3974, 2011.
SAS: SAS/STAT User's Guide: Version 9.4, SAS Institute Inc., Cary, NC, USA, 64, 2014.
Shafey, T. M., Mahmoud A. H., and Abouheif, M. A.: Dealing with multicollinearity in predicting egg components from egg weight and egg dimension, Ital. J. Anim. Sci., 13, 715–719, https://doi.org/10.4081/ijas.2014.3408, 2014.
Şahinler, S.: En küçük kareler yöntemi ile doğrusal regresyon modeli oluşturmanın temel prensipleri, Mustafa Kemal Üniversitesi, Ziraat Fakültesi Dergisi, 5, 57–73, 2000.
Tibshirani, R.: Regression shrinkage and selection via the lasso, J. Roy. Stat. Soc. (Statistical Methodology), 58, 267–288, 1996.
Topal, M., Eyduran, E., Yağanoğlu, A. M., Sönmez, A. Y., and Keskin, S.: Çoklu doğrusal bağlantıdurumunda ridge ve temel bileşenler regresyon analiz yöntemlerinin kullanımı, Atatürk Üniversitesi Ziraat Fakültesi Dergisi, 41, 53–57, 2010.
Uluocak, A. N., Okan, E., Efe, E., and Nacar, H.: Bıldırcın yumurtalarında bazıdış ve iç kalite özellikleri ile bunların yaşa göre değişimi, Turk. J. Vet. Anim. Sci., 19, 181–185, 1995.
Üçkardeş, F., Efe, E., Narinç, D., and Aksoy, T.: Japon bıldırcınlarında yumurta ak indeksinin ridge regresyon yöntemiyle tahmin edilmesi, Akademik Ziraat Dergisi 1, 11–20, 2012.
Yakubu, A.: Fixing multicollinearity instability in the prediction of body weight from morphometric traits of White Fulani cows, Journal of Central European Agriculture 11, 487–492, 2010.
Zou, H. and Hastie, T.: Regularization and variable selection via the elastic net, Statistical Society: Series B, 67, 301–320, 2005.





